Relativity – time for a change?
“The important thing in science is not so much to obtain new facts
as to discover new ways of thinking about them.”
William Lawrence Bragg
Introduction
A problem which plagued physics in the late 19th and early 20th centuries was the constancy of the velocity of light for all material observers. Einstein’s elegant solution in the Special Theory elevates light’s constant velocity to the level of a postulate followed by an investigation of the properties of space and time consistent with this postulate. Is there any reason to suppose that an alternative approach is possible given that conventional special relativity has been described both as “mathematically impeccable“ and “Beyond a shadow of a Doubt.“
There are at least three philosophical pointers indicating that a search for an alternative theory may not be fruitless:-
1. Popper suggests that irrespective of the number of experimental results agreeing with theoretical predictions we are never able to confirm a theory but merely fail to falsify it.
2. Leibnitz’ philosophy suggests that any finite number of observations can be accommodated within an indefinite number of explanations.
3. Locke urged us never to accept authority merely because it is authoritative unless by our own efforts we reach the same authoritative conclusions.
None of these statements indicate where to look for a new theory but they all hint that the search may be worthwhile. Furthermore as Prokhovnik points out
“… the logical perfection of a theory does not necessarily imply that it describes nature accurately – only that it is a reliable instrument for drawing conclusions from a given set of assumptions supposedly consistent with observation.”
(S J Prokhovnik, p85-86, The Logic of Special Relativity, CUP, 1967)
We are also encouraged in our search by the fact that, even now, (general) relativity has yet to be fully reconciled with quantum theory leading to Bell’s remark that perhaps a new conceptual approach is needed to further progress the unification of the two major theories which underpin almost the whole of modern physics.
In attempting to revise special relativity three ideas emerged each of which lead us further away from the conventional theory. Chronologically they occurred in the following order:
1. a closer look at the concept of velocity and the properties of light with reference to this view
2. an examination of how we measure time intervals with particular reference to clock readings
3. the existence of a particular inertial frame from which to view the behaviour of a system of masses.
However the easiest to describe and understand is an examination of how we measure time intervals so we shall consider this first.
Part 1
Analysis
The measurement of time intervals
The contents of this section are elementary and the mathematical outcome trivial but it may be of some value to state the basics of time measurement with a view to analysing conventional special relativity theory and developing a possible alternative. What we mean by time here is that number which results from merely counting clock periods. This is discussed in greater detail on the Time page.
In general any time period Δτ can be measured by any number of clocks according to the equation
Δτ = n1t1 = n2t2 = …… = nmtm (1)
shown graphically in Fig1, where all clock readings nm are set to zero at the start of the time interval.
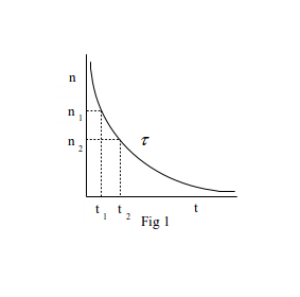Only when clocks are calibrated so that their periods, t, are the same can we use their readings, n, as a measure of the relevant time interval Δτ. This is exactly why we define an international standard of time so that our clock readings are meaningful in this respect.
We note that the curve illustrated in Fig 1 is a rectangular hyperbola and rotating this figure anticlockwise by 45° and re-drawing the vertical and horizontal axes reproduces the familiar Minkowski diagram of Fig 2.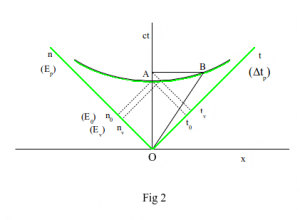
OA is the world line of observer A and OB is the world line of observer B moving at velocity v relative to A. The hyperbola shown is really the superposition of two curves; the green curve represents the hyperbola of Fig 1 and the black curve the hyperbola of a conventional spacetime diagram. The dotted lines show the mapping of B’s time on the vertical ct-axis to a clock period tv on the t-axis and also, via the green hyperbola, to a clock reading nv on the n-axis. Similarly A’s time maps on to clock period t0 and reading n0.
We can see in principle how observer B’s clock runs more slowly than observer A’s clock because period tv is greater than period t0; conversely clock reading nv is less than n0. This interpretation is consistent with the conventional view that clocks slow down with increasing velocity. At the speed of light they cease working altogether as tv, in Fig 2, approaches infinity when v approaches c; alternatively nv approaches zero as v approaches c.
We obtain a more general relationship than that given in Eq 1 by considering the quantity action, A, given by A = EΔτ, where E is energy and Δτ is a time interval. If we assume that any process, p, whether physical, chemical or biological is associated with a characteristic, constant action Ap, then the expression
Ap = Ep Δτp (2)
is the relationship between the energy Ep essential for the execution of that process in time interval Δτp, assuming the simple case of constant Ep.
Eq 2 expresses a principle of constant action.
We can now return to Fig 2 and re-label the n and t axes – clock readings and periods respectively – with our new variables Ep and Δτp. We now see that if a reduction occurs in energy available, for a process associated with observer B, then more time is required for its execution. This happens as B’s velocity increases relative to stationary observer A, in accordance with Eq 2, as illustrated in Fig 2. We will establish later a mechanism for such a decrease in available energy.
The elementary ideas presented in this section suggest the possibility that special relativity succeeds in deriving a relationship between process rates and velocity rather than time and velocity. Meanwhile the contents of this section act only as a pointer in the direction towards which our new model must develop.
So how did the idea became firmly established that time, rather than process rates, slow down with increasing velocity? The answer lies with the mathematics of the special theory which succeeds in finding properties of space and time consistent with the constancy of the speed of light for all inertial observers. By carefully examining the concept of velocity and the operational process by which it is measured we may reach a different conclusion.
Light and velocity
Our conventional and classical definition of velocity is based on the observed – and therefore presumably measurable – behaviour of material objects as they move through space. Thus the velocity of one material object with respect to a second is defined as the rate of change of distance between the objects with respect to time ie v = ds/dt with all the usual conventions. Fundamental to this definition is the ability to track the second object as it moves through space so that a measure of its changing distance (ds) can be obtained, at least in principle. That this is possible relies on a fundamental property of matter in that it marks its own position in space because space alone contains no landmarks. Reichenbach (The Philosophy of Space and Time, Dover Publications, 1958) points out that this fundamental property forms the basis of special relativity and introduces the concept relative in the expression relative velocity. The fundamental property of matter essential to its marking ability is that matter possesses mass.
In contrast to material objects light (electromagnetic energy) does not have the ability to mark space; it does not have mass. Light in its movement through space cannot be seen even in principle. Light is a non-material, mass-less, electromagnetic process detected, in principle, by a minute loss of energy at the material emitter and detected, in principle, by a minute increase in energy at the material detector. What happens between emitter and detector can never be monitored in the way it can for a material particle travelling through space. In this respect we might refer to the photon as a virtual (non-material, mass-less) particle in contrast to a real (material, massive) particle such as a proton.
Put simply matter can be seen during its progress through space but light cannot. This fact, that light in the process of propagation cannot reveal its location in space, will be referred to as the no-mark property of photons or electromagnetic radiation.
As stated our conventional definition of velocity implicitly assumes that we can measure the changing distance, ds, between relatively moving material bodies. This changing distance between objects can be measured by using light (radar), or some other appropriate method, but cannot be measured for light itself. Even light detected at the material particle which is the detector can only have its velocity operationally determined from our knowledge of the distance between the emitter and detector at the time of emission and the interval of time, dt, which has elapsed between emission and detection. Here distance and time interval measurements are (for the moment) made with reference to the space and time axes of the detector. Furthermore this characteristic of light – that its movement through space is undetectable – suggests that the velocity of receding light is not operationally definable. Light receding from an emitter cannot be tracked on its path through space as can a material particle. Therefore there exists no operational process by which we can continuously track receding light in its movement through space so we cannot measure its changing position, ds. Consequently the velocity of recession of light is not defined in contrast to that of a material body.
We cannot even measure the velocity of approach in the same manner as for a material body whose progress through space can be continuously monitored. Thus any changes to the velocity of an incoming material projectile can in principle be measured by radar for example. Light, however, simply disappears at the emitter and reappears at the detector. What happens in between cannot be measured whichever way it is moving.
A further consequence of the no-mark property of light is that no material object can move away from or closer to light in its journey from emitter to detector. The concept of movement implies the ability to detect and measure changes in distance. We cannot measure distance to an incoming photon or electromagnetic wave front because these entities do not mark their own locations in space. It is this (non-)property which guarantees that the velocity of light is the same for all observers. Movement amongst observers may be measured and quantified but movement of any observer with respect to light cannot be measured. It takes some effort to get used to this peculiar notion partly because we can imagine a photon on its path between emitter and detector but we have no means of actually tracking it in its progress. Worse still we can estimate its in-flight location and place a photo detector in this position, even after emission of the photon, and so actually detect it. In so doing we are interfering with its progress through space – it cannot continue on its path – and so the arguments with respect to its in-flight location transfer to the space between the original emitter and this newly introduced photo detector where again it cannot be tracked.
We are led to conclude that the only data available about the photon relating to its movement is the event which signals its emission and the later event which signals its arrival at the detector – that is at the start and end of its journey. If we know the distance s between emitter and detector at the instant of emission τe – in the detector’s frame – and the instant of detection τd – again measured in the detector’s frame – then the speed is simply c = s / (τd – τe).
(Knowing the value of τe is not without its own problems.)
Note that the value of c is independent of the relative velocity of the emitter and detector and is, of course, a speed of approach.
In quantum theory aspects of the treatment of light bear a striking resemblance to its no-mark property. Feynman’s Sum of Histories (Path Integral) approach to the analysis of light’s behaviour requires us to consider every possible route light can take from emitting source to detecting absorber. When interference effects from all these routes are taken into account only paths very close to the classical straight line path of light sum constructively; all other paths result in destructive interference and so contribute nothing to the final result. Using this technique allows Feynman to assert that:
“I can guarantee you… that every phenomenon about light that has been observed in detail can be explained by the theory of quantum electrodynamics…”
(Richard P Feynman, p38, QED The Stange Theory of Light and Matter, Penguin Books, 1985)
Another quotation used by Bacry is also pertinent:
“In order to illustrate all the difficulties encountered by the photon concept, let us quote and comment [sic] parts of an interesting text of M. Sachs in [Hoo]. It starts as follows: “ A very old, yet unresolved problem in physics concerns the basic nature of light… Still, logical dichotomy and mathematical inconsistency remain in the usual answers to the question: What, precisely, is light?” A few pages later, he is underlying [sic] conceptual difficulties: “But a single photon, which by definition, has a precise energy, is described mathematically in terms of a plane wave – a function that has an equally weighted value at all points in space at any given time. With this description, then, one would have to say that the single photon is everywhere, rather than somewhere – although it can be annihilated somewhere by looking for it at that particular place!…””
(Henri Bacry, p36, Localizability and Space in Quantum Physics, Springer-Verlag, 1988)
[Hoo] refers to:
(C.A. Hooker, Ed, Contemporary Research in the Foundations and Philosophy of Quantum Theory, Reidel, Dordrecht-Holland, 1973)
No-mark seems to be a compact version of the meaning distilled from these quantum theoretic examples.
If this is so it raises the question, in recognizing the non-localisation of light, has anyone thought to retrospectively modify SR in the light(!) of this peculiar quantum characteristic?
Comparisons with conventional theory and the ideas so far discussed in this section are illustrated in the following diagram, Fig 3. Each of the three parts a, b, c show four sets of world lines of two observers A and B, where A is the leftmost of each pair. The two horizontal dotted lines running through the figures represent a time interval τ. We should also note that the separation, s, of the two observers at the instants of emission of light is the same in each case. Adopting the convention c = 1 makes τ and s equal lengths in Fig 3.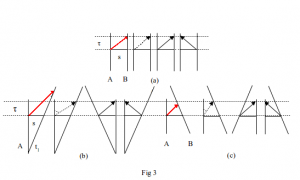
Fig 3a is a trivial example illustrating the exchange of light signals between relatively stationary observers. The red line depicts the conventional way of drawing light moving from A to B – emitter to detector – which we have suggested is problematic. The next part of Fig 3a shows the red line replaced by a dotted black line which we will adopt as the preferred way of illustrating this ‘undefined’ velocity of recession. The third part shows a full line – a velocity of approach – indicating that this exchange is viewed from the rest frame of observer B, the detector. Finally the fourth part shows light passing from observer B to observer A, now the detector, and so this too is correctly shown as a full line.
Fig 3b shows a similar exchange of light signals but this time A and B are moving away from each other. Again the red line shows the conventional way of drawing this signal in the first part of the diagram. The second part shows how the signal should be represented when drawn with respect to emitter A. As before it is a dotted line indicating that, as a velocity of recession, it is not properly defined; note it is also drawn with a slope greater than 45°. This is consistent with the third part of Fig 3b where the exchange is correctly viewed from the rest frame of the detector, observer B, and drawn as a full line at 45°. Again the fourth part shows light passing from observer B to A, in the rest frame of detector A, and so this too is correctly shown as a full line at 45°.
Fig 3c shows the exchange of light signals between A and B when they are moving towards each other. Once more the red line shows the conventional way of drawing this signal in the first part of the diagram. The second part shows it as a dotted line, a velocity of recession, drawn with respect to emitter A; note that the slope is less than 45° (s/τ = c = 1). This too is consistent with the third part of Fig 3c where the exchange is correctly viewed from the rest frame of detector B and drawn as a full line at 45°. The fourth part again shows light passing from B to A, in the rest frame of detector A, and so this is correctly shown as a full line at 45°.
The most important factor illustrated in these diagrams is the time taken for light to pass between A and B when they are in relative motion. This is independent of their relative velocity and dependent only on their distance apart at the instant of emission of the light signal as shown by the interval τ in Fig 3. Conventionally we expect this time to be greater than τ when A and B are separating and less than τ when they are converging as illustrated by the red lines of Fig 3b and c. This significant departure from convention is a direct result of the no-mark property of light. Furthermore it suggests that clocks traditionally associated with A and B in Fig 3, experience the same time interval τ common to both inertial frames. We shall discuss this further under the heading Common Time in a later section.
One situation not covered in Fig 3 is where the eventual detector moves relative to the emitter after light is emitted. For example light emitted from the sun has over 8 minutes before reaching Earth so what happens to light if, initially bound for detector A, another body, D, is moved in front of A within that 8 minute period? The explanation is quite lengthy and adds little to our attempt to seek a new approach to special relativity and so is presented in the Appendix to part I. It is best read after further developing the new light geometry introduced in Fig 3 particularly with reference to the classic Doppler Effect.
An analogy
The essential effect of no-mark is perhaps best illustrated by a crude mechanical analogy.
Imagine an emitting observer A stationary with respect to a receiving observer B. Each hold in their hand one end of a frictionless, threaded metal rod. At emitter A a frictionless nut is screwed onto the end of the rod. The nut represents a photon about to be emitted by A who strikes the side of the nut to start it rotating relative to the axis of the rod. The nut travels along the rod at a constant speed relative to both A and B determined by its rate of rotation and the pitch of the rod’s thread. The time taken, in B’s frame, for the nut to travel along the frictionless rod to B is determined by both of these factors and the length of the rod.
Suppose now that the nut and rod are not only invisible but undetectable. For the sake of the analogy we may suppose that they become invisible the instant the nut starts its journey along the rod. Now neither A nor B have any means of detecting this nut (photon) as it travels along the rod until detectability is restored when the nut arrives at B. Assuming the pitch of the rod and the rate of rotation of the nut are constants of this nutty universe then the time for the nut to travel along the rod is determined solely by its length ie the distance separating A and B at the instant of emission.
We may further suppose that in repeating this experiment B starts to move away from A at the instant of emission as A releases his grip on the rod; B maintains his grip in spite of the rod’s supposed undetectablilty. Once again, in B’s frame, the time taken for the nut to travel along the rod is determined by the length of the rod ie the distance apart of B from A at the instant of emission; it is unrelated to the increasing distance between A and B due to B’s movement relative to A. The nut is undetectable in transit so neither A nor B can measure its instantaneous speed. Only B can calculate the average speed of the nut along the rod from knowledge of the initial distance between A and B and the time elapsed, on B’s clock, between emission and B’s successful detection.
It only takes a moment’s reflection to realise that the above argument applies equally to movement of B towards A provided the speed of approach of B relative to A is less than the speed of approach of the nut towards B. The speed of the nut relative to detector B must be greater than any speed B can achieve in approaching A.
This latter condition completes the analogy between the undetectable, frictionless nut and a photon.
In the above description we must of course assume that in some unspecified manner B’s clock reading is known when the nut starts its journey. We can overcome this problem of knowing the time at two separate locations in space by imagining A is both emitter and detector. In this case the rod at B’s end is free so that when the nut reaches the end of the rod it automatically reverses its direction of rotation and ‘reflects’ off the free end of the rod and travels back to A. Thus A times the out and back journey of the nut with one clock and so can calculate the average speed of the nut just as we do with light reflecting from a mirror.
It seems important to note that the speed of the nut – and hence photon – results from a calculation of an average speed rather than a direct measurement of an instantaneous speed which is not possible because of the constraint imposed by the condition of no-mark or undetectability. This is part of the qualitative difference between the speed of light and the speed of material objects highlighted by the no-mark property.
Geometry and the Doppler Effect
We shall consider the case of a detector receiving hypothetical “signals” from a distant emitter moving with velocity v in the detector’s rest frame. These signals reach the detector in a time dependent on:
-
the distance x separating emitter and detector at the instant of emission
-
their speed of approach kc relative to the detector.
The first assumption is consistent with the no-mark hypothesis. In the second assumption c is the speed of light and k is a number in the range 0< k ≤ 1; this generalises the following analysis which can be made light specific by setting k = 1 in Eq 3 below.
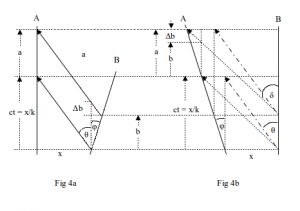
Fig 4 is a space-time diagram with x = kct and so x/k = ct. The “distances” b and a represent the time intervals between the two emitted “signals” and the two detected “signals”. They may also be taken as representing the period – or several periods – of a sinusoidal signal so the relation ship between b and a should be equivalent to that of a classical Doppler effect when k = 1. Figs. 4a and 4b are drawn respectively from the rest frame of the detector A and emitter B.
From Fig 4a we can deduce the following relationships:
a = b + Δb
Δb = btanφ / tanθ
a = b ( 1 + tanφ / tanθ ) (A)
and from Fig 4b 
a = b + Δb
Δb = atanφ / tanδ
a = b / ( 1 – tanφ / tanδ ) (B)
From the lower section of Fig 4b we obtain the relationship
ct tanδ = x tanδ /k = x + x tanφ / k
which simplifies to
tanδ = k + tanφ
Substituting for tanδ in (B) above and simplifying gives
a = b ( 1 + tanφ /k )
From Fig 4b we have tanφ = v/c and tanθ = k so finally (A) and (B) become
a = b ( 1 + v / kc ) (3)
Eq 3 is based on the generalisation that the emitted “signal” has a velocity kc relative to the detector. Only by setting k = 1 does Eq 3 give the conventional classical Doppler expression for a light signal received from a relatively moving emitter. This is equivalent to a value of θ = 45˚ in Fig 4 by which we conventionally represent the world line of light on a space/time diagram.
We note that when k = 1 and δ = θ Fig 4b becomes the conventional spacetime diagram for light signals sent from a stationary emitter to a relatively moving detector. Under these circumstances (B) above becomes
a = b / ( 1- v/c )
which only approximates to the classical Doppler effect of
a = b(1 + v/c) for v << c.
From the above analysis we conclude that a new light geometry based on the no-mark hypothesis is consistent with the classical Doppler Effect whether calculated from the rest frame of either detector or emitter.
A mathematical note
Before moving on we must make one further observation concerning the velocity of light. The no-mark property emphasises the qualitative difference between the velocity of light and the velocity of material bodies. Should we then mirror this difference in our mathematical representation of c? We can achieve this by making c an imaginary number ic just as material bodies have velocities represented by real numbers u, v, w. Resistance and reactance are similarly treated in AC theory. In doing this we can use a conventional Argand diagram to represent both real and imaginary velocities as shown in Fig 5.
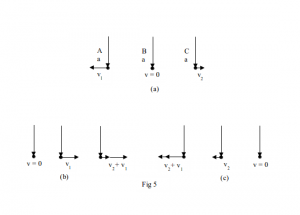Here Fig 5a shows 3 material bodies A, B, C each detecting an incoming light signal shown by the vertical lines with downward pointing arrows – imaginary velocities of approach. A and C are seen from the rest frame of B with real velocities shown as horizontal lines v1 and v2 respectively. Figs 5b and 5c show the view from the rest frames of A and C. Note how the change of rest frame alters the (real) relative velocities of A, B and C but leaves unchanged the (imaginary) velocity of light in any frame. We are assuming that the summation of velocities in this diagram is consistent with that in classical mechanics which, in terms of our model, has yet to be established. This assumption does not affect the present argument. If the assumption fails it simply means a different numerical value will attach, for example, to v1 + v2 rather than its classical value.
So far it is not clear whether the velocity of light is best represented mathematically as an imaginary number; this will also have to wait for confirmation as we develop our model. However Fig 5 serves to illustrate how the concept of an imaginary velocity may be used to provide a mathematical interpretation for the constancy of c consistent with a physical interpretation based on the no-mark property. This is conceptually different from special relativity which solves this problem with the indefinite metric of spacetime and the Lorentz transforms.
It is interesting to note in passing that Einstein, in developing the general theory, thanked Minkowski for the transform x4 = ict by which 4-dimensional space-time, of indefinite metric, becomes a 4-dimensional Euclidean space. Thus σ2 = x12 + x22 + x32 – c2t2 transforms to σ2 = x12 + x22 + x32 + x42.
He said that by virtue of this transform
“the [general] theory perforce gained clearness in no mean measure”
and shortly after
“Without it the general theory of relativity …… would perhaps have got no further than its long clothes”.
(Albert Einstein, Relativity, Methuen & Co, 1983, p57).
By associating the imaginary operator i with the velocity constant c rather than the time variable t we can perhaps gain some assurance that the concept of an imaginary velocity of light is not inconsistent with general relativity.
Common time
In moving from Newtonian physics to the physics of the special theory we lose the concept of absolute time and replace it with that of relative time. We are now able to consider a position somewhere between these two with the concept of common time. This we will do with the aid of the k-calculus introduced in the early 1960’s by Bondi. A full explanation of this technique is available in his book Relativity and Common Sense and even appears in such elementary text books as Patterns in Physics first published in 1974.
We can illustrate the use of Bondi’s method by combining the first and fourth parts of Fig 3b as shown in Fig 6a. In using the no-mark property of light we move to Fig 6b which is equivalent to combining the second and fourth parts of Fig 3c.
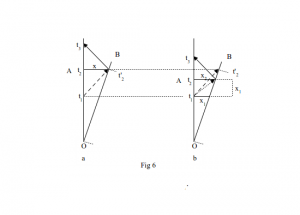Bondi originally assumed the following relationships which effectively define k for Fig 6a and can equally well be used to define a different value of k for Fig 6b.
k = t’2/t1 = t3/t’2
giving
t1 = t’2/k
and hence
t3 = k2t1
Here t1 is the observed reading of A’s clock when A sends a light signal to B which is received by B at observed reading t’2 according to B’s clock. Similarly B immediately sends back a light signal to A which is detected by A at t3 according to the observed reading of A’s clock. Bondi then asks what is the calculated reading t2 on A’s clock when B detected and immediately re-emitted the light signal at the observed reading t’2 on B’s clock? Both clocks are set to t = 0 at O (Bondi actually sets his clocks to 12:00). The calculation requires that A and B regard their relative speed as having the same value v and for them both to regard the speed of light as the same. Obviously in Fig 6a both regard the speed of light as c; in Fig 6b, because of the no-mark property of light, A calculates the speed of light from A to B as c+v, the dotted line, and similarly B calculates the speed of light from B to A as c+v, not shown. Fig 6b is drawn from the rest frame of A and so light returning to A from B is correctly shown as a speed of approach with the value c. The following table compares the calculations.
|
Fig 6a |
Fig 6b |
|
x2 = vt2 = c(t3 – t2) |
|
|
t3 = t1 + 2(t2 – t1) = 2t2 – t1 = k2t1 |
t3 = t2(c + v)/c = k2t1 |
|
hence t2 = t1 (1 + k2)/2 |
hence t2 = t1ck2/(c + v) |
|
x = vt2 = c(t2 – t1) giving t2 = t1c/(c – v) (a) |
x1 = vt1 = c(t2 – t1) giving t2 = t1(c + v)/c (b) |
|
thus k2 = (c +v)/(c – v) or k = {(c +v)/(c – v)}½ |
thus k2 = (c + v)2/c2 or k = (c + v)/c |
|
and from (a) t2 = t’2c/ (c – v)k = t’2/(1 – v2/c2)½ = γ t’2 |
and from (b) t2 = t’2 (c + v) /ck = t’2 |
From Fig 6a we derive the relationship t2 = t’2/(1 – v2/c2)½ = γ t’2 and from 6b we get t2 = t’2. The difference between these results is due directly to the no-mark property of light and suggests both observers experience the same common time interval albeit in situations which may allow different process times (clock periods). In this respect our concept of time is closer to that found in Galilean spacetime rather than that in Newtonian physics with space and absolute time.
The relationship t2 = γ t’2 derived from Fig 6a refers to clock readings. It states that B’s clock reading will always be less than A’s by the factor 1/ γ. Although Bondi states clearly that the two clocks are set to zero (12:00) at O we have to assume that they are synchronised to tick at the same rate at the velocity v, the velocity of recession of B with respect to A. See below for Einstein’s method of producing this synchronisation.
Assuming that the clock periods are generally ta and tb respectively and that initially the moving clock is synchronised with the stationary clock so that both have clock periods ts for a given value of v.
Hence
t2 = n2 ta = n2 ts
and
t’2 = n′2tb = n’2 ts
after Eq 1 where n2 and n’2 are A and B’s clock reading at times t2 and t’2.
From the table of calculations for Fig 6a, we have t2 = γ t’2, and so
n2 = γ n’2
That is B’s clock reading is always smaller than A’s by the factor 1/ γ as previously stated.
Suppose now that the clock periods are only identical when both clocks are relatively stationary and that B’s clock period may vary with v.
Hence ta = tb(v=0) but ta ≠ tb(v>0).
We can now write
t2 = n2 ta and t’2 = n’2 tb
and from the table of calculations for Fig 6b, where t2 = t’2, we have
n2 ta = n’2 tb
We now introduce a further assumption that tb = γ ta which states that the period of the moving clock (B) is longer than the period of the relatively stationary clock by the factor γ. With this assumption, based at this stage on empirical evidence, we can write
n2 = γ n’2
which is exactly the same expression obtained earlier. A theoretical derivation of our empirical assumption (tb = γ ta) is given in a later section.
From this we conclude that conventional theory and light geometry produce the same result for synchronised clocks as that with non-synchronised (but identical) clocks and the new light geometry based on the no-mark property of light. There is however a significant philosophical difference. In the special theory we interpret the result as a ‘slowing down of time’ for relatively moving objects; now we have an alternative explanation that ‘time’ is the same for everyone but moving clocks (processes) simply tick (proceed) at a slower rate with respect to relatively stationary ones. We shall see later in Section II that the value of v used in determining γ is a velocity measured in the centre of mass frame of the system of masses to which observers A and B belong.
The calculations relating to Fig 6a are in agreement with the special theory but Bondi’s k-calculus method is flawed if we accept the no-mark property of light. There must therefore be some point in the special theory where an equivalent flaw occurs.
In Einstein’s original paper On the electrodynamics of moving bodies he takes two separate but relatively stationary clocks and assumes a light signal sent from clock A (tA) is reflected at clock B (tB) and returned to clock A (t´A). Hence if the two readings of clock A and the single reading of clock B are related by the expression tB – tA = t´A – tB then the clocks are said to be synchronised given that the velocity of light is the same in both directions. We can then call two separate events at locations A and B simultaneous if the readings of previously synchronised clocks at A and B are the same. Einstein then assumes we are given a rigid rod and a measuring-rod by which we determine the length of the rigid rod to be l. Although no diagrams are used in the original paper Fig 7a summarises the synchronisation of clocks A and B assuming that the light signal is sent from one end of the rigid rod and received back there after reflection from the other end. This is not exactly what Einstein describes but it helps in comparison with the situation he did describe when the rigid rod is in motion as in Fig 7b.
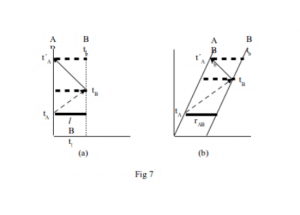Here he assumes the rigid rod moves at a constant velocity v along the x axis of a relatively “stationary” system of coordinates in the direction of increasing values of x. The ends of the moving rod he labels A and B and its length, measured in the stationary system is rAB, not necessarily the same as l. Furthermore there are clocks at either end of the moving rod which “synchronise with the clocks of the stationary system, that is to say that their indications correspond at any instant to “time of the stationary system” at the places where they happen to be”.
This is a device by which moving observers at either end of the moving rod can, by reading these moving clocks, directly access the times of the stationary system. He then says that a light ray departs from A at tA is reflected from B at tB and reaches A again at t´A producing the following relationship
tB – tA = rAB/ (c – v) and t´A – tB = rAB/ (c + v) (3)
consistent with Fig 7b.
Thus in the stationary system observers say the moving clocks are synchronised but moving observers with the moving clocks say they are not synchronised ( Fig 7b and Eq 3 where tB – tA ≠ t´A – tB). Einstein then concludes that events simultaneous in one frame of reference are not simultaneous in a relatively moving frame and thus establishes the relativity of simultaneity.
In Fig 7b and Eq 3 Einstein assumes that light travels from A the whole length of the moving rod plus the distance the end of the rod moves before light eventually reaches B. It also travels less far on the return from B to A because the point of detection, A, moves towards the approaching light. Neither of these assumptions is justified assuming the no-mark property of light. The terms (c – v) and (c + v) in Eq 3 are therefore inappropriate and should be properly replaced with c. Thus tB – tA = t´A – tb even if rAB ≠ l.
The relativity of simultaneity can no longer be maintained.
The problem in the original paper was to assume that movement can occur of a material object relative to a wave front of light. This false assumption leads to the conclusion that light has to travel further than the length of the moving rod on its journey from A to B and less than the length of the rod on its return from B to A. This same assumption is maintained in Bondi’s treatment, Fig 6a, with the result that the out and back distances light travels are the same whereas with the no-mark property the outward journey is shorter than the return one.
Virtually all methods of deriving the Lorentz transforms fail because none take into account the no-mark property of light. They range from Einstein’s original paper to Bondi’s k-calculus method almost 60 years later and beyond. Some absolute methods of deriving these transforms are discussed in Spacetime & Electromagnetism by J. R. Lucas and P. E. Hodgson (Clarendon Press, Oxford, 1990). These methods are based on the ordering relation causal influenceability and seem free from the above criticism. However they assume the existence of the past and future light cones of conventional theory. Although the past light cone is legitimate in the sense that it properly represents, at least locally, the world lines of incoming light rays the future light cone cannot be legitimately sustained in its conventional form. As indicated by the dotted lines showing the light paths in Figs 3b, 3c and 6b the angle which the ‘future’ light cone makes with the vertical time axis depends on the velocity of the detector relative to the emitter – again due to the no-mark property of light. In other words the future light cone cannot be drawn until we know both the identity of the detector and the velocity of the emitter relative to the detector. Its pre-existence as a fixed world line cannot be assumed as required in absolute methods of deriving the Lorentz transforms. These transforms, together with the relativity of simultaneity which they embody, are not consistent with the no-mark property of light. Is it asking too much too abandon such widely accepted concepts? Not according to Tim Maudlin who writes:
“Indeed, the cost exacted by those theories which retain Lorentz invariance is so high that one might rationally prefer to reject Relativity as the ultimate account of space-time structure.”
(Tim Maudlin, p220,Quantum Non-Locality and Relativity, Blackwell, 2nd edition, 2002)
Simultaneity
According to Reichenbach (The Philosophy of Space and Time) Einstein was the first to note that there is a degree of arbitrariness in the definition of simultaneity. Thus in Fig 6a the time for light to travel from A to B and back again to A is t3 – t1. If we know the distance x we can calculate the speed of light as
c = x / 2(t3 – t1)
This figure is actually the average speed of light for its out and back journey for we must make the reasonable assumption that the speed is the same in both directions. To calculate the outward speed we need to know the time according to A’s clock when the light reaches B; this incurs the problem of knowing the time at a distant location B. Reichenbach argues that to know this time requires knowledge of the speed of the signal (light) sent from A to B. The circularity of this argument, he says, can only be resolved by a definition. We can write a general expression for the time t2 in Fig 6a as
t2 = t1 + ε (t3 – t1) or ε = (t2 – t1)/(t3 – t1)
If we define ε = 1/2 we have t2 = ( t3 + t1 )/2. This is what Einstein did and in so doing made the ‘reasonable assumption’ that the speed of light is the same in both directions. It is interesting to note that the no-mark property of light provides us with a value for ε without an arbitrary definition.
From the table relating to Fig 6b we have t3 = k2t1, t2 = t1ck2/(c + v) and k = (c + v)/c. Using these relationships we can re-write the above expression for ε as
ε = ((t1ck2/(c + v)) – t1)/( k2t1 – t1)
which after simplifying and rearranging produces
ε = 1/(2 + v/c) (4)
Hence no arbitrary definition of ε is required.
We can now write
t2 = t1 + (t3 – t1 )/(2 + v/c) (5)
By setting v = 0 in Eq 5 we recover Einstein’s relationship t2 = ( t3 + t1 )/2 without an arbitrary definition of ε but this only applies to the exchange of light signals between relatively stationary observers. We might expect this result because the condition (v = 0) is the only one in which the light geometry used in the special theory agrees with the new light geometry appropriate to the no-mark property.
It is also worth noting that Reichenbach (p 156) argues that the relativity of simultaneity is not a necessary consequence of the special theory.
“It is true that one can define simultaneity differently for differently moving systems, which incidentally is the reason for the simple measuring relations of the Lorentz transformation, but such a definition is not necessary. We could arrange the definition of simultaneity of a system K in such a manner that it leads to the same result as that of another system K′ which is in motion relative to K; in K′, ε would not be equal to ½ in the definition of simultaneity but would have some other value. It is a serious mistake to believe that if the state of motion is taken into consideration, the relativity of simultaneity is necessary. Actually the relativity of simultaneity has nothing to do with the relativity of motion. It rests solely on the existence of a finite limiting velocity for causal propagation.”
If any doubts remain about abandoning the relativity of simultaneity Reichenbach’s words offer some reassurance. He even suggests that the “error committed in certain relativistic presentations lies in the belief that an absolute theory of time is logically impossible”. He goes on to state that absolute time could exist in a causal structure which “leads to a unique simultaneity”. His condition is that “there is no finite interval of time between the departure and return of a first-signal [light]” ie that t3 – t1 is zero in Fig 6a. The no-mark property, which allows us to determine ε and therefore maintain that t2 = t’2 in Fig 6b, provides a causal structure that “leads to a unique simultaneity”, though not quite in the manner suggested by Reichenbach, because ε is a variable dependent on v not an arbitrarily defined constant as generally assumed.
After more than a century of physics in which it has been almost universally accepted it takes a great effort to abandon the concept of the relativity of simultaneity. However the property of entanglement, which emerges from quantum theory, has always posed problems for this concept – see for example ‘Speakable and unspeakable in quantum mechanics’, J .S. Bell, CUP, 1987. We should also note, on a similar theme, the recent comment that:
“The kind of nonlocality one encounters in quantum mechanics seems to call for an absolute simultaneity, which would pose a very real and ominous threat to special relativity.”
( Albert and Galchen,p32, Scientific American, March 2009)
We are further encouraged by another remark from Tim Maudlin:
“But discovering a truly relativistic theory that can deal with Bell’s inequality is an exceedingly difficult task, and the theories presently available entail such severe dislocations of our physical view that one must seriously consider whether our grounds for adhering to Relativity are really strong enough to justify such extreme measures.”
(Tim Maudlin, p239,Quantum Non-Locality and Relativity, Blackwell Publishing, 2nd edition, 2002)
The no-mark property of light and its consequences (which include abandoning the Lorentz transforms) hints at a way round these problems and, by removing the necessity of Lorentz invariance, could perhaps herald a new era in future attempts to produce a theory of quantum gravity.
So far we have tried to establish that the special theory, in its conventional form, is not consistent with the no-mark property of light. We must now attempt to use no-mark to construct a plausible alternative and recover those tried and tested relationships, from the special theory, which experiment has failed to falsify. In particular we must recover the relationship E = mc2 and show exactly how γ relates the period of moving clocks (etc) to relatively stationary ones; in this treatment we have so far only accepted these as empirical relationships. Having already abandoned the relativity of simultaneity and the Lorentz transforms we must perhaps also be prepared to jettison other concepts and relationships regarded as central to conventional theory.
But you would expect no less from off-piste physics.