Rel Part II

 

Part II

Synthesis

“Be open to ideas and thoughts you disagree with.

It will unleash a debate in your mind and soul.”

James Kirk Bisceglia

Ancient Treasure

A preferred frame of reference

We have already discussed some fundamental ideas about the relative velocity of material bodies and accept that these velocities may be viewed from different inertial frames – see for example the real velocities of Fig 5 – without compromising the fact that c is the same in all frames. However if we send a rocket away from Earth we feel, with some justification, that it is the rocket which is moving and not us. This is based on the view that we maintain (more or less) our location in space relative to near and distant masses but the speeding rocket changes its relative location. Thus on a journey to the moon an obvious change in location has occurred for the rocket and its crew. On returning to Earth another change of location has occurred for them but not us. From the crew’s point of view they may be justified in regarding themselves as stationary but could not escape the conclusion that, relative to near and distant masses, it is they who change location not us. In spite of the existence of the crew’s rest frame, relative to which they can describe the universe about them, is their situation truly symmetrical with respect to their Earth-bound fellows? One conventional argument states that a lack of symmetry follows from the change of inertial frames for the crew, one on the outward journey and another on returning, whereas those back on Earth have remained in just one inertial frame. Alternatively, to achieve their change in location, the rocket crew must have undergone an acceleration to leave Earth, a deceleration and re-acceleration to return to Earth and a further deceleration to land back on Earth. It is these accelerations that are the source of the asymmetry. Both sources of asymmetry have been used to resolve the so-called clock paradox, a comprehensive and critical discussion of which is available at

http://web2.utc.edu/~tdp442/paradox.pdf

We can address this problem by initially considering the fiction that the universe consists of one single mass point. Here the concept of (translational) movement becomes meaningless because there is nothing relative to which this movement can be measured. Adding a second mass point improves matters to the extent that movement of either mass relative to the other can now occur. Having established two masses a third classically unique point can be defined relative to these masses and this is their common centre of mass. What happens if we consider motion of these objects from the inertial frame whose origin P, Fig 8, is this centre of mass?

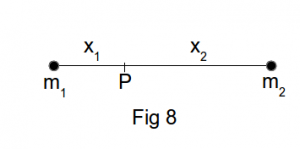P is defined by the relationship

      m₁x₁ + m₂x₂ = 0.

Suppose a gravitational interaction occurs between the two masses resulting in a change in the distance between m₁ and m₂. As a result of the accompanying change in x₂, m₂ acquires a velocity v₂, relative to P; similarly m₁ acquires a velocity v₁ relative to P. Classically the relationship between these velocities is given by

m₁v₁ + m₂v₂ = 0              (4)

Momentum is conserved in this classical centre of mass frame and P is its origin. For the moment we accept that masses m₁ and m₂ are independent of velocity. In this frame we do not have to judge which of the two masses is moving because if one moves relative to P then both move relative to P to conserve momentum. If we set up material axes at P complete with a clock C_p then, from conventional theory, backed by experiment, we expect equivalent clocks on m₁ and m₂ to run more slowly than C_p however, in general, v₁ ≠ v₂ so these clocks also run at different rates from each other. Does this imply that clock rates depend on velocities measured in the centre of mass frame not the relative velocity of one mass with respect to another? In discussing the related centre of momentum frame Rindler (Essential Relativity Springer-Verlag, 1979 revised second edition, p 85) points out that in non-Newtonian mechanics the centre of mass is frame dependent because the mass of each particle varies in moving from frame to frame. This assumes, in agreement with conventional theory, that mass m₂, say, is dependent on the relative velocity of m₂ with respect to m₁. In what follows we will show that it is possible to maintain the dependence of mass on velocity but in a quite different manner from that of the original theory and consistent with the classical concept of a centre of mass frame.

So far, although critical of special relativity, we have assumed that it correctly predicts variations in process rates with increasing velocity. In other words we have assumed that γ = 1 / (1-v²/c²)^½ but have yet to derive this relationship in terms of the present model. We have used the conventions of the traditional space-time diagrams by adding to the 3 dimensions of space a fourth dimension, ct, by which we introduce time. In this context c is a constant of proportionality, relating distance to time, having the numerical value of the speed of electromagnetic radiation. As such we shall refer to it, somewhat pedantically, as c_α, and interpret this as implying that every item of mass in the universe, in the 4^th dimension (c_αt) of our model, is associated with a parameter c_α having the units of velocity. This, for example, is consistent with an expanding soap bubble model of the universe where the two dimensional curved surface of the bubble is equivalent to our 3 dimensions of space. As the bubble expands all matter in its surface moves further away from its centre at the same speed as indeed it must to remain in this undistorted spherical surface. The centre of the expanding bubble suggests there was a time when the universe was small and in a more dense, compact state (the origin of the big bang?).

For each item of mass in this universal 3-dimensional surface the product mc_α has the dimensions of momentum even though mass m is not necessarily associated with any conventional momentum resulting from movement in 3-space relative to some other mass.

We will call this value of m  the universal mass m_u and its associated momentum p_u = m_uc_α.

This allows us to distinguish between conventional theory which uses rest mass m₀ and our new model which uses m_u.

Let us further suppose that the total (4-space) momentum associated with each m_u is conserved  just as conventional 3-space momentum is conserved, over all masses, in the centre of mass frame of classical mechanics as in Eq 4.

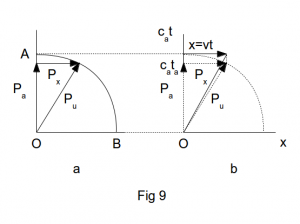
Fig 9a shows the relationship between total momentum p_u and its components p_x = m_uv and p_α where p_α is the component along the c_αt axis.

For brevity p_x represents the vector sum of p_x + p_y + p_z.

The axes of Fig 9a have the units of momentum and can be transformed into those of Fig 9b by multiplying by a factor with dimension [TM^-1], specifically t_a/m_u.

Thus

p_x = m_uv

becomes

p_xt_a/m_u = vt_a = x

and

p_u = m_uc_α

becomes

p_ut_a/m_u = c_αt_a.

We can now compare the diagram of momentum space, Fig 9a, with that of space-time, Fig 9b. The dotted line representing the p_x vector in Fig 9b is shown as the same length as the full line representing the x = vt_a vector. This is achieved by choosing an appropriate scale for the momentum vectors or alternatively – and perhaps more generally – by considering p_u, p_α and p_x as representing momentum per unit mass and t_a as a unit period of time.

Thus

x = vt_a → v

and

p_x = m_uv → p_x/ m_u = v (numerically).

It is evident from Fig 9a that p_α is given by

p_α = (p_u² – p_x²)^½

                = (m_u²c_α² – m_u²v²)^1/2

                = m_uc_α (1 – v²/c_α²)^½

         = p_u/γ_α                   (5)

Note that the negative sign in the expression for γ_α in Eq 5 follows from our assumption that p_u is conserved. In other words as mass m_u acquires velocity v in its centre-of-mass frame its total momentum vector rotates (in momentum space) but maintains the same magnitude (ie length) in spite of an increase in 3-space momentum p_x due to velocity v.

In special relativity this negative sign appears as a result of the indefinite metric of spacetime with its characteristic  signature (+ – – – or – – – +), from which we derive the Lorentz transforms. Fig 9 is drawn in essentially a 4-dimensional Euclidean space with its characteristic Euclidean signature (+ + + +). Conventionally the observed constancy of the speed of light for relatively moving observers is consistent with the Lorentz transforms. In the new model the no-mark property of light achieves the same result which is consistent with a mathematical representation of the speed of light as an imaginary number as suggested in Part I.

Returning to Fig 9 and Eq 5 we assume a momentum exists along the c_αt axis. In doing so we have simply extended the classical concept of momentum with its three separate p_x, p_y, p_z, components to include a fourth component p_α. This is similar to the procedure adopted for relativistic 4-vectors but these use a differential coefficient based on the spacetime interval dσ where

-dσ² = c²dτ² = c²dt² –dx² – dy² – dz²

giving

dt/dτ = 1/(1 – v²/c²)^½ = γ

(see p188, Spacetime & Electromagnetism ).

In our model the four components of momentum are related to the total momentum, the magnitude of which we have assumed is conserved, by the expression

p_u² = p_x² + p_y² + p_z² + p_α².

Thus when p_x = p_y = p_z = 0 then p_α = p_u, taking the positive square root, as in Fig 9.

We also note from Eq 5 that p_α = p_u/γ_α producing the relationship p_α = m_αc_α = m_uc_α/γ_α giving

m_α = m_u/ γ_α           (6)

where m_α is the effective “component” of mass associated with the c_αt axis and momentum p_α. As real velocity v approaches real velocity c, m_α approaches zero and so prevents further increase in v. We should repeat here that, at this stage, v is the velocity of m_u in the centre of mass frame of the system of masses to which m_u belongs. In conventional theory we have the expression m_v = γm₀ where m_v approaches infinity as v approaches c but here v is a velocity measured in the rest frame of some other massive particle. From this we deduce that there is at least a conceptual difference between rest mass m₀ and universal mass m_u.

Rest mass is the mass of a body at rest in its own inertial frame whereas universal mass is the mass of a body at rest in the centre of mass frame of the system of masses to which it belongs. For example the Earth, Moon and all other matter orbiting the Earth constitute a local mass system whose centre of mass (barycentre) lies below the Earth’s surface. The Sun and planets and all matter orbiting the Sun constitute the system of masses for the solar system. Its barycente sometimes lies within the body of the Sun but often somewhere ouside the Sun’s surface. See for example:

https://spaceplace.nasa.gov/barycenter/en/

Momentum and energy

Before considering more fully the energy associated with the total momentum and its components we must establish a method for determining the kinetic energy of a body whose mass varies according to Eq 6. A brief review of both classical and conventional relativistic derivations of kinetic energy provides a technique for this calculation.

Kinetic energy is defined as the energy required when accelerating a body mass m, from rest to some velocity v, equivalent to a momentum change from zero to mv. The value obtained is frame dependent and for a system of masses is (classically) a minimum in the centre-of-mass frame of the system of masses.

Classically the calculation is carried out by assuming the mass is subjected to a force F operating over an infinitesimal distance dx. The work dW done by this force is then equal to the energy dE acquired by mass m.

Hence

F.dx = dW = dE

Force F is defined as the rate of change of momentum dp/dt giving

dE = (dp/dt).dx

If mass m is moving at velocity v then

dE = (dp/dt).vdt = v.dp

Integration then gives the kinetic energy of mass m.

E = ∫v.dp        (7)

Eq 7 can be used to calculate both classical and relativistic kinetic energy.

a. Classically p = mv where m is assumed to be constant.

In this case we have

E = m ∫v.dv

       = mv²/2 + K

 where K is the constant of integration.

We know that when v = 0 then E = 0 so K = 0 giving the classical formula for kinetic energy as

E = mv²/2

b. Relativistically p = m_vv where m_v = m₀( 1- v²/c²)^-1/2 = γm₀ ie both m and v are variables.

Eq 7 becomes

E = ∫v.d(m_vv)

      = m₀∫v.d(γv)

                  = m₀∫v.(vdγ + γdv).

From the expression for γ we get dγ = (vγ³/c²)dv and substituting for dv in the above expression gives

      E = m_o∫v.(vdγ + (c²/vγ²)dγ)

= m_o ∫(v² + c²/ γ²)d

         = m_o c² ∫(v²/c² + 1/ γ²)dγ

              = m_oc² ∫(1 – 1/ γ² + 1/ γ²)dγ

= m_oc²∫dγ

Hence

E = m_oc²∫dγ

     = γm₀c² + K

When v = 0 γ = 1 and E = 0 therefore K= -m_oc² giving the conventional relativistic kinetic energy as

E = m₀c²(γ -1)

This is an important result which is supported by experiment.

c) In our model we require an expression for kinetic energy where velocity has a fixed value c_α and mass varies as m_α = m_u/γ_α. That is the kinetic energy of a body whose momentum is given by

p_α = p_u/ γ_α = m_uc_α/ γ_α

Eq 7 now becomes

E = ∫c_α.dp_α

               = m_uc_α² ∫d(1/γ_α)

              = m_uc_α²/ γ_α + K.

Kinetic energy is defined as the energy required for momentum to increase from zero to some value p. In this case p_α = 0 and so E_α = 0 when γ_α = ∞ (v = c) therefore K = 0.

Hence E_α = m_uc_α²/ γ_α            (8)

This is the classically derived value of kinetic energy for a particle of varying mass m_α = m_u/ γ_α and constant velocity c_α. It is consistent with our model which requires any mass to maintain a velocity component c_α, numerically equal to c, in the c_αt dimension. Any variation in the magnitude of the momentum component p_α can only result from a corresponding change in mass m_α.

The expression for E_α given in Eq 8 can be traced back to our assumption that total momentum p_u, associated with any mass m, is conserved.

Noting once more that γ_α = 1 when v = 0 then from Eq 8, by writing E_{α (v = 0)} = E_u, we recover perhaps the most famous equation in physics (due allowance being made for the subscripts α and u)

E_u = m_uc_α²

Perhaps this provides some justification for our assumption that the magnitude of p_u is conserved.

d) We have shown that E_α can be obtained by considering a mass m_α = (m_u/γ_α) associated with a constant velocity c_α. This is consistent with a momentum p_α = (m_u/γ_α)c_α. So far we have considered the 3-space momentum – represented by p_x – to have it’s classical value m_uv. However since p_α has a mass component m_u/γ_α should we not expect to use the same mass component for p_x? To preserve the value of p_x we must further assume that the velocity component of p_x is γ_αv.

We now require the kinetic energy of a mass with momentum p_x = mv → (m_u/γ_α) γ_αv where

dp_x = d(mv) = d(m_u/γ_α) γ_αu.

The derivation of this shows that, unsurprisingly, dp_x = m_udv which leads to the expected classical value of momentum as in section (a) above. This redundent calculation establishes some peace of mind about the use of a  velocity component  γ_αv which, however,  still requires further explanation. This result is consistent with the idea that the classical momentum p_x is derived from a mass m_u/γ_α and a velocity component γ_αv.

In mechanics the technique used in a, b and c above to derive an expression for kinetic energy assumes that inertial mass is used in all calculations. The expression for E_x which is consistent with our model therefore suggests that inertial mass varies as 1/γ_α but this variation is masked by the additional requirement that γ_αv should be used in calculating momentum component p_x.

We can write the expression for E_u in terms of  momentum and velocity as

E_u = m_uc_a² = m_uc_a x c_a = p_u c_a.

We have already assumed the conservation of p_u and so E_u must also be conserved as the product of a conserved momentum and a velocity constant c_a. E_u, in our model, is equivalent to the rest energy E₀ of conventional special relativity. E₀ is the energy of a mass at rest in its own inertial frame whereas E_u is the energy of mass at rest in the centre of mass frame of the system of masses of which it is part. These two values will be numerically equal because any mass at rest on the surface of the Earth will also be at rest with respect to the Earth’s centre of mass, neglecting the common effects, if any, of the earth’s rotation and gravitational potential.

More needs to be done before reaching a firm conclusion regarding the energy associated with our moving  body even though we have recovered the energy-mass relationship and the classical 3-space momentum p_x.

We must now consider our 4-space momentum vector and what it takes to produce its rotation whilst conserving its magnitude in spite of an increase in 3-space momentum p_x and energy E_x.

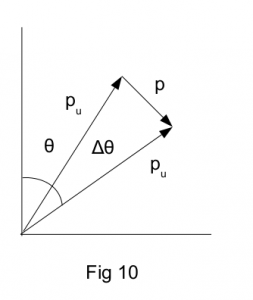
From Fig 10 we can write the vector equation

   p_u = p_u + p

or

p_u – p_u = Δp_u = p

Also from Fig 10

p/sinΔθ = p_u/sin(90 – Δθ/2) = p_u/cos( Δθ/2)

therefore

p = p_u sinΔθ/cos( Δθ/2)

In the limit as Δθ and  Δp_u → 0

dp_u = p_udθ.

If all this happens in time dt then

dp_u/dt = p_udθ/dt.

In terms of this (neo)classical analysis we can interpret dp_u/dt as the force F_θ required to rotate the momentum vector, magnitude p_u, through the infinitesimal angle dθ; the direction of this force is perpendicular to p_u.

We have F_θ = p_udθ/dt and from Fig 9 v/c_a = sinθ giving dv = c_a cosθ dθ which combine to give

F_θ = p_u(1/c_a cosθ)dv/dt

   = m_u(1/cosθ)dv/dt

=γ_vm_udv/dt.

But m_udv/dt is the classical value of a Newtonian force F_N

therefore

F_θ = γ_vF_N

As  v→0, θ→0, γ_v →1

and

F_θ →F₀ = F_N

TO BE CONTINUED