About Space
“We are all agreed that your theory is crazy.
The question which divides us is whether it is crazy enough to have a chance of being correct.
My own feeling is that it is not crazy enough.”
Neils Bohr
First steps
Every physical theory has to start from somewhere and with something. The usual primitives are space and time with matter added shortly afterwards. Although we may have a basic understanding of what we mean, conventionally, by space and time, or even Minkowski’s spacetime, these concepts are associated with a long history of philosophical debate.
A particular problem with space is the nature of its existence and what properties, if any, it possesses. A mathematician or philosopher may be happy to accept that it has no sensible attributes but a physicist attempting to construct a theory from a space which is unobservable, indiscernible and possesses no landmarks, is presented with something of a challenge. Recognising this Minkowski writes:
“Not to leave a yawning void anywhere, we will imagine everywhere and everywhen there is something perceptible. To avoid saying “matter” or “electricity” I will use for this something the word “substance.” We fix our attention to the substantial point which is at the world point x,y,z,t, and imagine that we are able to recognize this substantial point at any other time.”
( Einstein, Lorentz, Weyl, Minkowski, p76, The Principle of Relativity, 1952, Dover Publications.)
He starts with a yawning void but quickly fills it with substance, eschewing alternatives like “matter” or “electricity”, before properly embarking on his seminal paper ie before he starts theorising about physics. This probably marks the real beginning of special relativity and in effect pointed Einstein towards the general theory with its emphasis on geometry.
It seems a little odd, not to say problematic, to base physics on such a tenuous concept as space. Physics is perhaps primarily concerned with the behaviour of matter, the way it interacts and the means by which this interaction occurs. The traditional view is that the existence and behaviour of matter occurs in space; matter acts out a drama in the theatre of space. If physics’ main concern is the properties and behaviour of matter is it possible to abandon space and time initially and posit matter as the beginning of physics?
Maudlin cautions against this approach when he states:
“And we could, with Leibnitz and Mach, somehow try to eliminate space-time as an entity altogether, but it nevertheless plays an essential role in the formulation of physical theory. There is no more call to try to eliminate space-time structure from physics than there is to eliminate the postulation of atoms, just because they cannot be seen.”
(Maudlin T, p66, Philosophy of Physics Space and Time, Princeton University Press, 2012)
But what happens if we actually attempt to follow Leibnitz and Mach? As Alexander remarks the 17th century mathematician Cavalieria thought that:
“mathematics begins with a material intuition of the world – that plane figures are made up of lines and volumes of planes, just as a cloth is woven of thread and a book compiled of pages.”
(Amir Alexander, p71, The Secret Spiritual History of Calculus, Scientific American, April 2014, vol 310, no 4).
So if mathematics ‘begins with a material intuition of the world‘ perhaps physics should also start with the same intuition.
Let’s begin with Minkowski’s “substance” but not dispersed through space like some continuous form of substantial aether. Instead we will consider this substance condenses into separate, solid, macroscopic agglomerations of finite size and to paraphrase Minkowski:
To avoid saying “substance” (or “electricity”) we will use for this something the word “matter”.
These solid objects we have produced – this matter – is now a perceptible something of finite extent. Here is our starting point and although we have arrived via Minkowski’s yawning void, filled with perceptible ‘substance’, there is no strict necessity for this. It merely demonstrates a close conceptual link between what has gone before and what is to follow.
So our physics now begins with something material – a substance – something we can literally and conceptually get to grips with because of its familiarity, ubiquity and discernibility. It possesses sensible properties in contrast to that indiscernible something called space.
Thus we have matter, by which we mean that which possesses mass and volume. Note we are not saying that it occupies a volume of space just that, of itself, it is “extended” and given a suitable metric we could quantify this extension and call it “volume”.
At this stage there is as yet no need to talk of space or time. We just have matter which is simply solid, perceptible “stuff” of finite extent with no hypotheses about its internal microscopic structure should it have one. In this respect we are embarked on the construction of a classical, elemental, model of physics whose primary construct is matter.
Consider first the inside of one of these finite, macroscopic, material objects. We discover that we can, in our imagination, move about in the interior in what we might recognize as three independent directions. This leads us to conclude that the interior of matter is 3-dimensional and continuing our internal investigation we further discover that it is bounded by a closed, possibly irregular, surface of only two dimensions. So matter exists within a bounded 2-dimensional material surface; what, if anything, exists outside the surface?
Logically we can say that it is NOT matter and if we allow ourselves the liberty of describing matter as a ‘thing’ then NOT matter is NOT a ‘thing’ or NO ‘thing’ or nothing. This nothing seems to be remarkably similar to Minkowski’s yawning void; so once again:
To avoid saying “NOT matter” or “void” we will use for this nothing the word “space”.
Whereas Minkowski started with a yawning void quickly filled with a perceptible something called substance we have started with a finite something called matter beyond whose boundary exists something called space. Have we simply arrived rather cheekily at the yawning void with which Minkowski started? Not quite as we shall see shortly. However at this primitive level it does seem possible to start doing physics with matter and quickly arrive at the concept of space as simply the absence of it.
What is the point of this approach if we end up with two concepts, matter and space rather than starting with space and then populating it with matter?
By starting with matter we bring space into existence as that which is outside or beyond the boundary of matter.
Space has no existence or meaning in this primitive model in the absence of matter.
Logically, in this model, matter takes priority over space because the existence of matter effectively brings space into being. To talk of empty space is meaningless in the physics of this model because the existence of space requires matter itself to exist. In this sense space is an emergent concept which surprisingly echoes current views on string theories. For example Nathan Seiberg writes:
“We summarize the arguments that space and time are likely to be emergent notions; i.e. they are not present in the fundamental formulation of the theory, but appear as approximate macroscopic concepts. Along the way we briefly review certain topics. These include ambiguities in the geometry and the topology of space which arise from dualities, questions associated with locality, various known examples of emergent space, and the puzzles and the prospects of emergent time.”
http://arxiv.org/abs/hep-th/0601234v1
It is also worth noting Einstein’s comment on the interpretation of GR:
“We are now in a position to see how far the transition to the general theory of relativity modifies the concept of space. In accordance with classical mechanics and according to the special theory of relativity space (space-time) has an existence independent of matter or field. In order to be able to describe at all that which fills up space and is dependent on the coordinates, space-time or the inertial system with its metrical properties must be thought of at once as existing, for otherwise the description of “that which fills up space” would have no meaning. On the basis of the general theory of relativity, on the other hand, space as opposed to “what fills space”, which is dependent on the coordinates, has no separate existence. Thus a pure gravitational field might have been described in terms of the gik (as functions of the coordinates), by solution of the gravitational equations. If we imagine the gravitational field, ie. the functions gik to be removed, there does not remain a space of the type (I) [Minkowski space-time] but absolutely nothing, and also no “topological space”. For the functions gik describe not only the field, but at the same time also the topological and metrical structural properties of the manifold… There is no such thing as an empty space, ie. a space without field. Space-time does not claim existence on its own, but only as a structural quality of the field.”
(Albert Einstein, p155, Relativity The Special and General Theory, University Paperbacks, Methuen, London, 1964 re-print)
Returning to the imaginary exploration of our piece of matter we can choose to move internally in a particular direction and on reaching the boundary continue to move beyond it. Here we discover, with reference (relative) to the three independent directions available for movement within matter, there are three similar directions available for movement in this region outside the matter boundary.
We conclude that this region also possesses three dimensions and so, in this respect, mimics the matter with which its existence seems so closely bound.
This raises an interesting question.
If 3-dimensional matter is bounded by a 2-dimensional surface marking the start of a 3-dimensional non-material region is this region bounded by a 2-dimensional surface marking the start of matter?
Is it the same surface?
At first sight this conjecture appears to be completely without foundation – ludicrous even – but consider the following analogies.
Let’s suppose that a piece of matter and the external region it gives rise to can be modelled as a droplet of water suspended in a very large volume of air (we will refer to this analogy as A1). The water droplet is our “solid” 3-dimensional matter bounded by a 2-dimensional closed surface and the air represents an apparently unbounded 3-dimensional non-material region. Now invert this model and suppose that we have an air bubble suspended in a very large volume of water (analogy A2). Here the air is a 3-dimensional region bounded by a 2-dimensional closed surface which is the boundary of an apparently limitless 3-dimensional “solid” – the water.
The two analogies used above are not entirely satisfactory in that there appears to be no natural way of moving from A1 to A2. This shortcoming is addressed as follows.
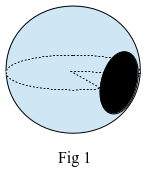
Fig 1 illustrates a balloon version of the model. The curved black disk is drawn on the 2-D surface of a balloon and represents matter (the water droplet) bounded by a 1-D surface (a line). The rest of the balloon’s surface represents a 2-D region (the air) bounded by the same 1-D surface (A1). We could also consider the black disk to be the air bubble with the rest of the surface (water) representing matter (A2).
What we are now describing is one matter/no-matter object with the topology of a sphere whose components, matter and no-matter, share the same boundary. This matter/no-matter structure brings to mind Minkowski’s fusion of space and time into spacetime. Just as matter is finite and bounded by a matter/no-matter interface so also is the no-matter region, finite and bounded by the same no-matter/matter interface. It is of some interest to note that this elementary model gives rise to a curved geometrical model whose curvature exists as a consequence of a shared matter/no-matter boundary.
This model emerges from the investigation of one piece of matter – or rather from the viewpoint of one piece of matter. Where do other pieces of matter fit into this picture? We attempt to answer this question later.
Meanwhile we should perhaps consider the following forceful remark, from 1982, by Julian Barbour:
“Minkowski, Einstein and Weyl invite us to take a microscopic look, as it were, for little featureless grains of sand, which, closely packed, make up space-time. But Leibnitz and Mach suggest that if we want to get a true idea of what a point of space-time is like we should look outward at the universe, not inward into some supposed amorphous treacle called the space-time manifold. The complete notion of a point of space-time in fact consists of the appearance of the entire universe as seen from that point.”
(Quoted in Brown, H R, p14, Physical Relativity, Oxford University Press, 2005.)
If we replace the expression “space-time” with matter/no-matter then the quotation above applies to our new model where the point from which the universe is seen is within, or on the surface or, the matter part of our composite object.
At this stage we should recognize that the region beyond the surface of a material object appears to be affected by something for which the object is the source, namely the gravitational field, or more fundamentally, the gravitational potential field. Whether matter produces the potential or the potential produces matter is a moot point.
We can now proceed to create a physics whose foundations rests not on spacetime but on the (pre)existence of matter and this region of no-matter called the gravitational potential field (not the gravitational force field).
Or can we?
Have we been too keen to resurrect the classical concept of space by following in Minkowski’s footsteps? Should we not take note of Einstein’s comment that without the gik nothing exists at all, not even a pre-existing empty space? In terms of our model therefore what exists outside the boundary of our piece of matter is the gravitational potential field produced by it. This brings us much closer to the concept of ‘field’ as used in quantum field theory. Thus the pre-existence of a gravitational potential field (formerly known as space) creates the fundamental, material building blocks of matter through quantum fluctuations of the field; quanta of matter – some sort of elementary particles – are to the gravitational potential field as photons – quanta of electromagnetism – are to the electromagnetic field.
Logically our approach has been to assume matter is primary and the gravitational potential field results from the existence of matter. The excuse for starting with matter arose solely from the requirement of getting rid of the classical concept of empty, indiscernible space. However our starting point should not be with an object based on the matter-space concept but rather a field-particle concept following Einstein’s interpretation of the mathematics of general relativity.
We can now view Fig 1 as a classical representation of a piece of matter, made up of a large number fundamental particles, and its associated gravitational potential field.
An obvious question arises. If matter and field are so intimately linked, as illustrated in Fig 1, how big is this object and where should the matter-field boundary be drawn?
So far we only have a topological version of the model in which either the extension of the field exceeds the extension of matter, A1 or vice-versa, A2. To get some idea of the relative sizes of this matter-field combination we have to introduce a metric into our model and a unit of length.
The metric
We will assume that we are dealing with a 4-dimensional manifold in which we can use, for simplicity, Cartesian coordinates. The distance relation is expressed as
ds2 = dx12 + dx22 +dx32 + dx42
and we shall use the Planck length as our unit of length.
We must now commit the minor sin of accepting relationships between physical properties which have not been established within the framework of our existing primitive model. These relationships are well established in conventional theory and for the moment we simply accept that they must be consistent with our present model for it to be viable.
They are:
the reduced Compton wavelength λr = ћ/mc
the Schwarzschild radius rs = 2Gm/c2
which combine together as
λr rs = 2G ћ/c3 = 2ℓp2 (1)
where ℓp is the Planck length.
The product of the reduced Compton wavelength and the Schwarzschild radius is simply of the form xy = constant, Eq1, which can be graphically represented as a rectangular hyperbola.
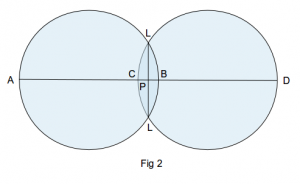
For our purpose it is helpful to recognise that we can derive a similar relationship from the geometry of a circle using Euclid’s chord theorem.
The vertical chord LL is common to both circles and bisected at P by the line AD giving us the following relationships:
AP x PB = PL2 = CP x PD
If we let PL = √2 ℓp then from Eq1 we can say AP = λr and PB = rs for the left hand circle and similarly CP = λr and PD = rs for the right hand circle.
The similarity between Fig 1 and the circles in Fig 2 is interesting.
By introducing into our model a metrical unit based on the Planck length we have created an interesting matter-space object whose actual size is mass-dependent by virtue of the relationships between mass, the reduced Compton wavelength and the Schwarzschild radius. We now consider a particular choice of these values where
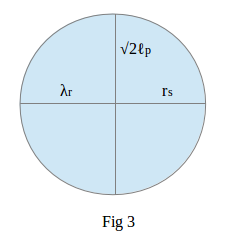
λr = rs = √2 ℓp
Fig 3 illustrates a matter-field object whose reduced Compton wavelength and Schwarzschild radius are equal with a value of √2 ℓp; this is greater than the Planck length by a factor of √2 and so is of the order 2.3 x 10-35 metres. It is as close as our model comes to a representation of the hypothetical Planck particle of conventional physics. Perhaps this gives us the liberty, with typical physicist’s whimsy, to refer to it as a planckton.
The mass of such an object is
m = ћ/c√2 ℓp = ℓp c2/√2 G = mp / √2 = 1.5 x 10-8 kg
which is the same order as the Planck mass usually defined as
mp = ( ћc/G)1/2 = 2.2 x 10-8 kg.
If we limit our interest to orders of magnitude in our model then the similarity between the values m and mp in the above two expressions allows us to refer simply to the Planck length and Planck mass in what follows.
This result is identical to that found at:
http://math.ucr.edu/home/baez/lengths.html#planck_length
but the author John Baez does not speculate further on the relationship as we do in what follows.
To continue
We can interpret Fig 3 as illustrating the existence of a boundary between matter with a λr greater than the Planck length and matter with an rs greater than the Planck length. The critical factor is the mass of the planckton represented by Fig 3.
Objects with masses less than (roughly) 10-8 kg have (reduced) Compton wavelengths which are larger than their hypothetical Schwarzschild radii; these radii have values forbidden by the Planck length limit so such low mass matter cannot form black holes. There is no general consensus that the Planck length does represent a limit to the smallest distance that has any operational meaning, but perhaps there should be. As long ago as 1964 at least one physicist made just such an assertion, see
C. Alden Mead, Possible Connection Between Gravitation and Fundamental Length,
Phy. Rev. 135, B849, 10 August 1964.
Objects with masses greater than 10-8 kg have Schwarzschild radii which are larger than their hypothetical (reduced) Compton wavelengths; these wavelengths also have values forbidden by the Planck length limit.
We seem to be at the boundary between quantum objects exhibiting wave-particle duality and gravitationally significant objects in the form of black holes. An interesting feature of our model is that it accommodates both types of matter with a smooth transition from one to the other. Even a black hole never quite escapes its quantum characteristics having a well determined reduced Compton wavelength albeit only of a hypothetical nature. Similarly a low mass object, exhibiting demonstrable wave-particle duality, has an equally well determined Schwarzschild radius also of a hypothetical nature.
The dual wave-particle nature of matter with mass less than 10-8 kg is mirrored by the particle-wave nature of matter having mass greater than 10-8 kg. As mass decreases matter exhibits more and more those properties we conventionally associate with the realm of quantum theory. As mass increases gravitational effects become increasingly dominant as we move closer to the classical world of everyday objects.
This raises the question why don’t masses greater than 10-8 kg always exist as black holes? We know that this doesn’t happen but Fig 3 implies that perhaps it should. However the electron, for example, has a mass-based Schwarzschild radius in the region of 10-57 m and a similar measurement based on its charge produces the figure 10-36 m; both values are much smaller than the Planck length so the electron can’t exist as a black hole. The same argument can be used for the other main components of ordinary matter, the proton and neutron. So whether we use classical physics to calculate these values or some version of quantum theory the building blocks of matter cannot exist as black holes and when they combine in various ways to form atoms, molecules and so on, the dimensions of the everyday objects formed will invariably be much larger than their Schwarzschild radii. Hence ordinary matter exists generally in this extended form. However the volume of a black hole is proportional to rs3 with the value of rs proportional to its mass. Hence doubling the mass increases the volume by a factor of 8. This means the average density, based on rs, decreases as the mass increases so black holes can form, given the right conditions, from suitably large agglomerations of ordinary matter.
Fig 3 illustrates the hypothetical lower limit for the total volume, matter plus space, of any matter-space object. Note that this is the volume of a 4-dimensional sphere whose radius is of the order of the Planck length.
We must now investigate the possibility of an upper limit for such an object.
The universe?
Once again we must borrow from conventional physics this time in the shape of the Heisenburg uncertainty principle in its equivalent forms:
∆p∆x ≥ ћ/2
∆E∆t ≥ ћ/2
with the usual conventions.
Essentially the second of these relationships tells us we cannot measure the energy of a particle or the time it has this energy with complete precision; the errors in these measurements, ∆E and ∆t, are always related as above. Similarly for momentum and position.
Thus any energy En is associated with an uncertainty of the order of ∆E implying that E lies in the range:
En ± ∆E
and cannot be known with greater accuracy.
We are dealing here with the energy associated with matter (mass) which again from experience and theory is, for m > 0, always positive and given by E = mc2. We can therefore say for m > 0 the minimum allowable energy Emin is such that
Emin – ∆E > 0
or
Emin > ∆E.
From the uncertainty principle the smallest value of ∆E occurs when ∆t is a maximum giving
Emin > ћ/2∆tmax.
The maximum possible value of the time interval ∆tmax is the age of the universe which is of the order 4×1017 seconds according to curent theory and observation, equivalent to a value for λr of approximately 1.2×1026 metres.
This gives a value for Emin of approximately 1.3×10-52 joules (7.8 x 10-34 ev), equivalent to a mass of roughly 1.4×10-69 kg an incredibly small quantity.
This value, which relies heavily on our current estimate for the age of the universe, sets a limit for the maximum size of our matter-field object based on the reduced Compton wavelength of a piece of matter with a mass of 1.4×10-69 kg, a truly quantum object. We arrive at this result by pursuing the logic of the uncertainty principle to the conclusion that we can never have precisely zero mass-energy, an exact value denied by that very principle.
The nature of the calculations used above are similar to those used to determine approximately the minimum energy required to confine a particle in a 1-dimensional box. That method uses the de Broglie wavelength, based on the momentum of the particle, rather than the (reduced) Compton wavelength based on the rest mass of the particle. See for example
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/pbox.html
and related calculations.
Is there a way of making an equivalent assessment based on the Schwarszchild radius ie a gravitational object?
Let us make an assumption, based on the symmetry of Fig 2, and propose that the maximum value of rs is the same as that for λr .
This leads to a value for the mass of the largest possible black hole consistent with our assumptions of
mmax = rsmax c2/2G
which is roughly 6.7×1052 kg.
The mass of the observable universe is often stated as close to 1053 kg from the following three calculations;
1. estimates based on critical density
2. observation from the number of stars
3. Hoyle’s steady state universe (with adjustments).
Given that all the calculations above are only approximations and in spite of the use of a rash, symmetry-based assumption for rsmax, the similarity of these figures demonstrate at the very least a surprising coincidence. It is tempting to speculate that a universe based on this model contains just the right amount of mass expected for a black hole of that size. This is not to suggest that the universe is a black hole rather that the physics of black holes, at this elementary level, is consistent with the physics of the universe treated as a whole. Students of the beauty of physical theories should note that this view offers a pleasing symmetry.
Comments
Perhaps the most counter-intuitive aspect of this model is the suggestion that something as large as the universe, with its mass-based relationship to a black hole, can be brought into existence by the smallest amount of mass-energy consistent with the uncertainty principle. Furthermore the object so formed is a quantum object having extremely low mass and very large Compton wavelength, reduced of otherwise.
We might be tempted to borrow from the Pythagoreans and call this fundamental unit of universal mass a monad – the first being or totality of all beings – an entirely appropriate use of the word when we consider that the views on “space” presented here have definite Leibnitzian overtones. This universal monad has associated with it all the “space” required to make up the whole of the universe. The remainder of the entire matter-field objects of the universe fit into this “space”. So our model provides a theatre akin to classical space in which matter can enact its drama based on fundamental assumptions quite at odds with the primacy of space in conventional cosmology. Before celebrating this minor achievement we should perhaps heed van Fraassen’s cautionary words:
“General relativity may indeed have so changed even the concept of space-time in physics as to make all previous philosophical analyses inapplicable. The space-time of special relativity….was still correctly conceived of as an independent arena, in which the pattern of events of our actual total world history (whatever it be) is located. The conception, as [in] the earlier ones of time and space, was that of a general form in which any physically possible world fits”
and shortly after
“In general relativity, it is no longer so. The models of this theory do not have a common space-time; they are space-times, and as its afficionados never tire of pointing out, exhibit an astonishing variety of structures. So the idea that space-time is the logical space we use to represent spatio-temporal distributions of matter-energy is, with its presuppositions that the two structures are independent, an anachronism.”
( van Fraassen Bas C., p 209, An Introduction to the Philosophy of Time and Space,
Columbia University Press/New York, 1985)
Perhaps we have so far avoided this anachronism by starting our primitive model with matter rather than space-time.
All of our matter-field objects should be referred to collectively as quons, a word coined and defined by Nick Herbert as:
“… any entity, no matter how immense, that exhibits both wave and particle aspects in the peculiar quantum manner.”
(Nick Herbert, p 64, Quantum Reality, Rider, 1985, )
With this interpretation everything is a quon, from plankton – the smallest – to monad – the largest – including all of us who occupy the classical middle ground as long as they exhibit “both wave and particle aspects”.
We must introduce a cautionary note here because a mass greater than the Planck mass has a physically unrealisable reduced Compton wavelength and cannot therefore be represented mathematically by a wave function. At least this saves Schroedinger’s cat from being in a dead/alive superposition; it is either dead or alive because it’s too heavy to be both.
For any of this to make scientific sense our model must provide testable predictions which differ from those of currently accepted models…
…and therein lies the challenge.
It should be noted that these ideas about “space” are not essential to the discussion of special relativity (see pages under Rel) which adopts, initially, a slightly more conventional spatial approach. The contents of this page are best viewed simply as an unconventional muse on the concept of “space” in its own right and is, of course, comfortably off-piste.